马尔可夫决策过程

我们下面学习动态决策：序列决策制定。有大量的应用都是这种决策，比如机器人、投资、运营。

本节学习经典的 Markov Decision Processes。这时，我们已知 Transition 和 Reward 模型，想要获得最优策略。我们学习两种算法：值回归和策略回归。

序列决策问题

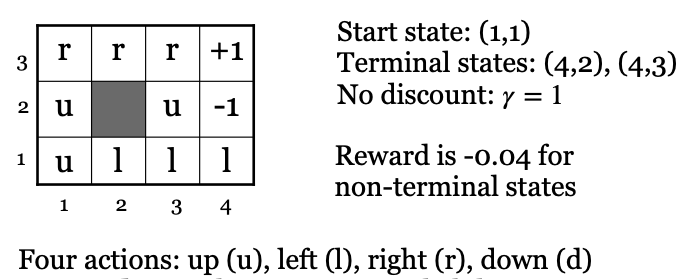
序列决策问题有三个重要概念：状态、动作和回报。下图画出了机器人路径规划问题。如图所示，机器人当前所处的位置，就是“状态”；它下一步的动作（上下左右），就是“动作”；它每走一步，要消耗一定的时间和能量，意味着这一步的“回报”是负值，而最终，当他胜利到达终点，会得到一个很大的“回报”，而且这个“回报”是正值。

我们再看一个公司决策的例子。下图画出了我们如果开办一家公司的话，我们的序列决策问题。如下图所示，我们的状态包括四个：没钱且无名；没钱但有名；有钱且无名；有钱且有名；我们的下一步动作有两种选择：储蓄还是做广告。储蓄会让我们有钱，做广告会花钱，但会让我们变得有名；“回报”呢？就是我们最后能不能盈利：只有我们变得富有了，才有“回报”。注意，没钱但有名，是没有回报的，但只有经历这个阶段，才能变得富有。请问，你在其中的哪个阶段呢？

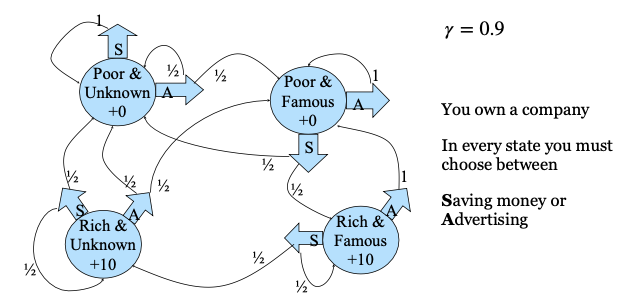
我们将上面举例的序列决策过程用数学模型描述，这就是著名的“马尔可夫决策过程（MDP）”。它由四个部分组成：状态（State）、动作（Action）、状态转移模型（Transition）、 回报模型（Reward）。它为什么叫“马尔可夫”呢？因为它的状态转移模型符合马尔可夫性。所谓马尔可夫性，就是下一步怎么样，只和当前状态有关：过去的，就让它过去；一切从现在开始。

因此，我们的目的是解决我们面临的序列决策问题，获得最高的回报。用数学的话说，就是已知 Reward 和 Transition 模型的情况下，求最佳策略（Policy）。所谓策略，就是在状态 S 下的最佳动作。

值函数

我们首先想到的是，这么多状态，能不能给每一个状态打一个分。那么这个分就可以给我们一个参考，我们就使劲朝着高分的状态走呗。为此，我们引入状态的“值函数”，用 \(V(s)\) 表示。在数学上，我们定义它为状态 s 按照当前 Policy 走下去的“效用”（utility）的期望。显然，让我们初始状态 s 的“值函数”最大的策略，就是我们的最优策略，对吧？

如果我们画出 MDP 模型的决策图，我们就会发现它是一个“非决定性的”概率搜索问题，而我们前面学过的搜索问题是“决定性”的搜索问题。此时，当已知 Transition 和 Reward 模型时，如何获得最优策略？我们有两种计算方法：值回归（Value iteration）和策略回归（Polity iteration）。我们下面分别介绍它们。

Value iteration

值回归方法通过回归的方法算出每一个状态的 V。下图画出了它的算法。

如上图所示，在初始化每个状态 S 的 V 后，它就开始迭代（for 循环）。在迭代的每一步，它都基于 Bellman 等式，更新每个状态 S 的 V。怎么更新呢？它计算这个状态下的各个 Action 能够获得的收益。这个收益包括执行这个 Action 立即能够获得的 Reward R(s,a) ，还包括执行这个 Action 后可能进入的下一个状态的 V 的期望。当然，这个期望会通过 \(\gamma\) 进行衰减。它最后选收益最高的 Action 的收益，将这个收益作为状态 S 的最新的 V。就这样一直迭代，直到 V 稳定下来，或者完成固定的迭代次数。这个过程，就叫“值回归”。

值回归能够用矩阵很方便地实现，如下图所示：

等 V 稳定下来后，按照 V，提取最佳 Action，就是最优 Policy 了。

总之，值回归方法会比较一个状态下的各种 Action 的结果，选出最大的，更新状态的 Value。伯克利 CS188 AI Lec 8 MDP I PPT 给出了 Value Iteration 的详细过程，非常直观、清晰、有趣。请参考该 PPT。

值回归方法会比较一个状态下的各种 Action 的结果，选出最大的，更新状态的 Value，这有三个缺点：首先，计算量很大，是 \(O(S^2A)\)；其次，它浪费：在计算的过程中，Max 的结果很少发生变化，所以很多计算都浪费了；最后，在 Value 收敛之前，Policy 早就收敛了，由此，它的很多计算没有必要。因此，人们提出了 Policy Iteration 方法。

Policy iteration

因此，我们可以换一种方法：首先初始化一个 Policy，然后就按照这个 Policy 往下实验。这样的话，每次在一个状态 s 下只会执行一个 Action。这时，我们就用这个 Action 后的“下一个状态”的值，来更新状态 s 的值。这样计算就简单很多。按照这种方法，迭代计算了每一个状态的值后，基于这些值，更新策略，选择期望 Reward 最高的 Action，这就得到了最新的策略。然后，再迭代该策略下，各个状态的值。然后再更新策略。这就是策略回归方法。伯克利 CS188 AI Lec 8 MDP II PPT 给出了 Policy Iteration 的详细过程，非常直观、清晰、有趣。请参考该 PPT。

因此，策略回归，是以优化 Policy 为中心。它也是采用迭代的方法，但迭代的是 Policy。它的算法如下图所示。

如上图所示，它的迭代包括下面的两步：

第一步是策略评估（Policy Evaluation）。此时，它计算在当前 Policy 下，各个状态的 V。计算方法是：基于当前策略，得到状态 S 要执行的 Action a，然后计算执行 a 之后得到的收益。这个收益的计算和“值回归”时的计算时一样的。这样，它就得到了当前策略下的各个状态的新的 V。

如果我们观察策略回归的公式，我们会发现它其实就是一个关于 V 的线性方程组，因此，可以用矩阵方法就可以直接求解。此外，策略评估的概念非常重要。我们后面还会用到它。

第二步是策略改进（Policy Improvement）。此时，它保持各个状态的 V 不变，更新 Policy。具体来说，它会往前看一步，计算每个状态下的各个 Action 的收益，然后寻找最大收益的 Action，将“选择它”作为最新的策略。它也被称为 Policy Extraction，因为是基于最新的 V 来提取新的策略。注意，它只会往前看一步，而不是像 Value 回归似的，迭代计算 V。

更新完 Policy 之后，它再回到第一步，计算这个新 Policy 下各个状态的值函数，然后再做第 2 步，如此迭代，直到 Policy 稳定。

因此，策略回归的方法就是：基于当前策略，做 Policy Evalation，得到各个状态的值，然后基于这些值，比较各个 Action，用能够获得最大值的 Action 作为最新的策略动作。我们可以证明它和 Value Iteration 一样，也是最优的。在大多数情况下，它比 Value Iteration 方法收敛得快很多。

策略回归也能够用矩阵很方便地实现，如下图所示：

Bellman 等式

Bellman 方程证明了值函数的一个基本性质：它满足一定的递归关系。该方程实际上有两个方程：贝尔曼期望方程和贝尔曼最优方程。其中，Policy Iteration 用了期望方程，而 Value Iteration 用了最优方程。

课程材料

课本材料

练习


Index Previous Next