Transformer

基于自注意力机制，人们提出了Transformer这一强大的序列模型。Transformer，这个名字来源于变形金刚，已经成为深度学习领域的标志性技术。目前，所有主流的深度学习模型几乎都是基于Transformer衍生出来的，应用范围非常广泛。

Transformer模型具体由两部分组成：编码器和解码器。下图画出了它的结构。

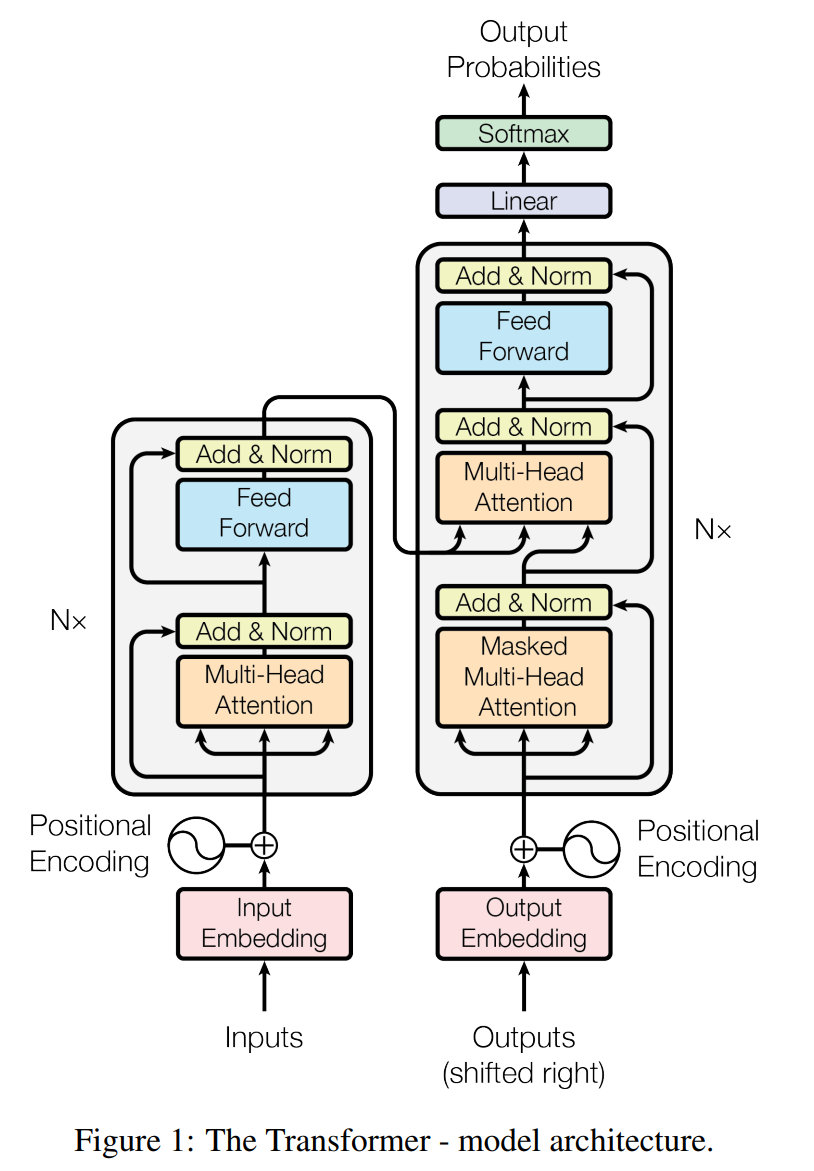
如上图所示，左边是编码器（Encoder）。它接收输入序列，并逐层处理这些数据，通过自注意力机制和前馈神经网络将其编码为一组上下文表示。右边是解码器（Decoder）。它接收编码器的输出，并结合目标序列，通过自注意力机制和前馈神经网络生成最终的输出序列。

我们下面来看编码器和解码器的具体设计

编码器

Transformer 的编码器由多个堆叠的自注意力块组成。下图是它的结构。

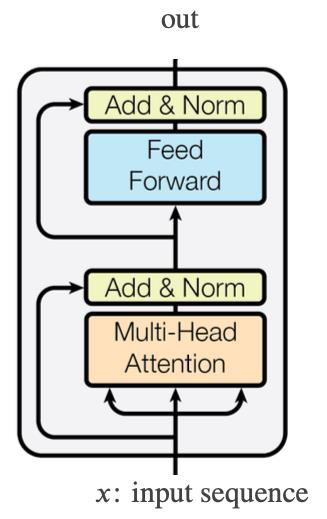
如上图所示，它包括以下三个设计：

  1. 多头注意力机制：类似于卷积神经网络（CNN）对一张图片，采用多个卷积核独立地进行卷积（即 Channel），Transformer 为每个单词训练多组注意力权重。这就是所谓的多头注意力机制。这是因为人们发现：一个自注意力头往往会聚焦到某一个词。因此，人们通过使用多个头（通常为8个），让一个单词能够查询更多的单词，从而改进模型的性能。

  2. 前馈神经网络层（FFN）：自注意力机制本身是线性的。为了增加模型的非线性能力，我们在注意力机制之后加入了非线性激活函数。具体来说，通过加入一个前馈神经网络，利用它的非线性激活函数，增加模型的非线性能力。

  3. 残差连接：在注意力机制和前馈神经网络之间加入残差连接。残差连接使得这两者之间的结合更加紧密，提高了模型的稳定性和性能。

通过结合多头注意力机制、前馈神经网络和残差连接，我们就获得了一个功能强大的注意力块。多个这样的注意力块堆叠在一起，就构成了 Transformer 的编码器。

解码器

在解码过程中，首先对解码输入序列进行自注意力处理。需要注意的是，这里的自注意力机制采用了 Masked 注意力。下图画出了 Masked 注意力机制（左小图）和一般的注意力机制（右小图）的工作机制。

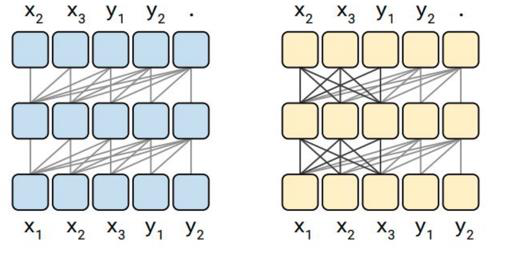
如上图所示，在 Masked 注意力机制中，一个 Token 只能“注意”自己位置的 Token，以及自己位置前面的 Token，不会“注意”后面的 Token。而一般的注意力机制的 Token 在“注意”起来的时候，没有这个限制。

这是因为在生成一个单词时，后面的单词信息尚未知道，因此不能将注意力集中在这些单词上。因此，我们通过使用Mask的方式，避免模型关注后面的单词。这就是所谓的Masked 自注意力机制。

它的实现如下：如果查询向量（Query, Q）的索引 \(i\) 大于键向量（Key, K）的索引 \(j\)，就将注意力分数设为负无穷，这样经过Softmax处理后，这个注意力关系就会被忽略。

在解码输入序列经过自注意力机制处理后，会被送入一个“跨注意力机制”，进行编码器和解码器之间的注意力处理。此时，查询向量（Q）来自解码器，而键向量（K）和值向量（Value, V）则来自编码器。跨注意力机制的结果，再经过前馈神经网络处理，生成最终的输出。

输入位置编码

自注意力机制的一个问题在于：输入序列中 Token 的先后顺序可能被忽略。因此，人们设计了各种“位置编码”方法，将 Token 的序号等位置信息引入模型。我们下面介绍两种方法。

三角函数位置编码

第一种方法是采用正弦（sin）和余弦（cos）函数进行编码，以获得 Token 的相对位置。该方法的基本思想是：将序列中每个位置 \(pos\) 设置一个固定维数的向量，比如 16 维。这个位置向量的取值如下：

\[PE_{(pos, 2i)} = \sin(\frac{pos}{10000^{2i/d_{model}}})\] \[PE_{(pos, 2i+1)} = \cos(\frac{pos}{10000^{2i/d_{model}}})\]

其中，\(PE\) 是位置编码，\(pos\) 是位置，\(i\) 是维度索引，\(d_{model}\) 是模型的维度。

为什么这种编码方式能够表示序列中 Token 位置的相对关系呢？让我们首先观察一个特定维度（比如 \(i=1\)）的位置编码。从公式中我们可以发现：当 \(i=1\) 时，位置编码是具有正弦和余弦形式的周期函数，也就是说，它的值会随着位置的变化而周期性变化。因此，当两个位置有着相同的编码值时，这意味着这两个位置之间的距离正好等于这个周期函数的周期的整数倍。这反映了两个位置之间相对距离的特定信息。

对于不同的维度 \(i\)，位置编码的周期是不同的。因此，所有这些不同维度的位置信息综合到一起，就表示了两个位置之间相对距离的不同尺度的信息。通过结合这些位置信息，模型能够准确地捕捉序列中 Token 的相对位置和顺序。这就是位置编码设计的基本原理。

旋转位置编码

我们接下来介绍一种最近非常常见的旋转位置编码（Rotary Position Embedding, RoPE）。下图画出了它的原理

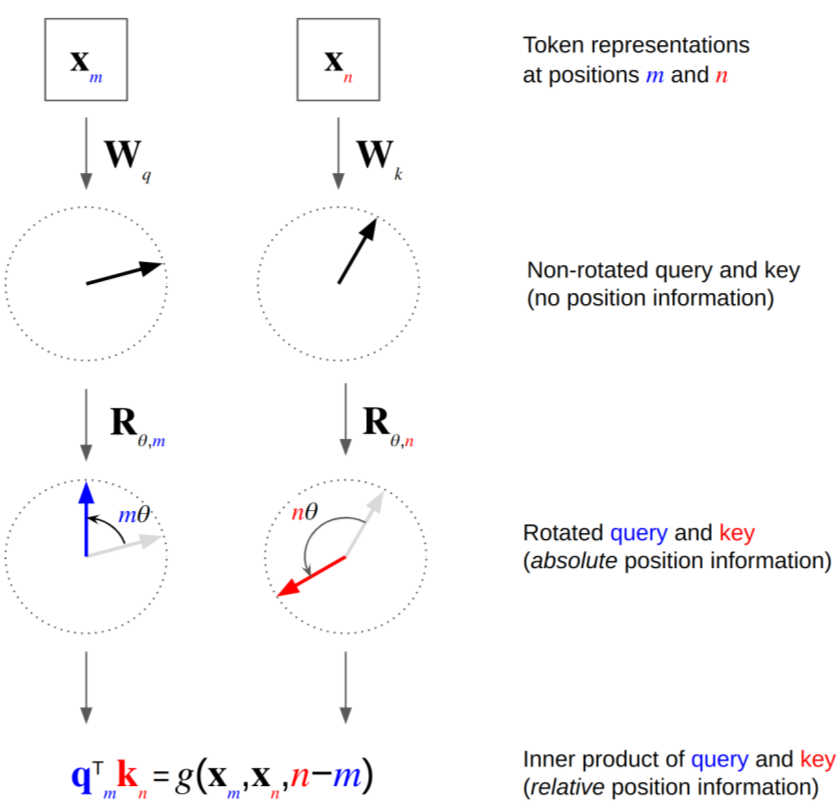
如上图所示，这种方法的原理是通过旋转输入向量的方式，将位置信息编码到 Token 中。其数学表达式如下：

设输入向量 \(x\) 的维度为 \(d\)，位置为 \(pos\)，则旋转位置编码 \(RoPE(x, pos)\) 的公式为：

\[RoPE(x, pos) = \left[ \begin{array}{cc} \cos(\theta_{pos}) & -\sin(\theta_{pos}) \\ \sin(\theta_{pos}) & \cos(\theta_{pos}) \end{array} \right] \cdot x\]

其中，\(\theta_{pos}\) 是与位置 \(pos\) 相关的角度，可以通过以下公式计算得到：

\[\theta_{pos} = \frac{pos}{10000^{2i/d}}\]

如上式所示，旋转位置编码（RoPE）首先定义旋转矩阵 \(R(\theta_{pos})\)：

\[R(\theta_{pos}) = \left[ \begin{array}{cc} \cos(\theta_{pos}) & -\sin(\theta_{pos}) \\ \sin(\theta_{pos}) & \cos(\theta_{pos}) \end{array} \right]\]

熟悉计算机图形学的同学会理解，如果我们将一个二维向量和上面的旋转矩阵相乘，就会在二维平面上把该二维向量旋转 \(\theta\) 度。因此，我们将旋转矩阵应用到输入 Token 的向量 \(x\) 上，就能得到旋转后的输入 Token 向量表示 \(x_{pos}\)：

\[x_{pos} = R(\theta_{pos}) \cdot x\]

这个向量就将输入序列中各个 Token 的位置信息融合到其向量表示中，希望后面的模型能够利用其中的位置信息。

Layer normalization

Transformer 还采用了 Layer normalization。该方法对一层的 \(a\) 的向量做归一化。这是因为在 MLP 中常用的 Batch normalization 在这里不太适用。首先，训练数据的 batch 小，然后，sequance 的长度不一样。

Transformer 还采用了层归一化（Layer Normalization）。该方法对每一层的向量 \(a\) 进行归一化处理。这是因为在多层感知机（MLP）中常用的批归一化（Batch Normalization）在这里并不太适用。首先，训练数据的批次（batch）通常较小；其次，序列的长度也不尽相同。因此，层归一化成为更好的选择。层归一化通过对每一层的输出进行归一化处理，可以有效地稳定训练过程，加速收敛，并且提高模型的整体性能。

层归一化（Layer Normalization）的数学公式描述如下：

设输入向量为 \(x\)，其维度为 \(d\)。层归一化的步骤如下：

  1. 计算输入向量的均值 \(\mu\) 和方差 \(\sigma^2\)： \(\mu = \frac{1}{d} \sum_{i=1}^{d} x_i\) \(\sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2\)

  2. 对输入向量进行归一化处理： \(\hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}\)

其中，\(\epsilon\) 是一个很小的常数，防止分母为零。

  1. 对归一化后的向量进行缩放和平移，得到最终的输出： \(y_i = \gamma \hat{x}_i + \beta\)

其中，\(\gamma\) 和 \(\beta\) 是可训练的参数，用于缩放和平移归一化后的向量。

通过上述步骤，层归一化能够有效地提高模型的训练稳定性和性能。

小结

Transformer 模型有以下几个优点：

由于这些优势，Transformer 模型在深度学习领域得到了广泛应用，几乎成为了主流。例如，像 ChatGPT、腾讯元宝都采用了 Transformer 架构。

然而，Transformer 也有其不足之处。其注意力机制的计算复杂度为 \(O(n^2)\)，这对计算资源提出了很高的要求。此外，如前所述，它也需要大量的数据。

课本

课程材料

复习题

练习

参考


Index Previous Next